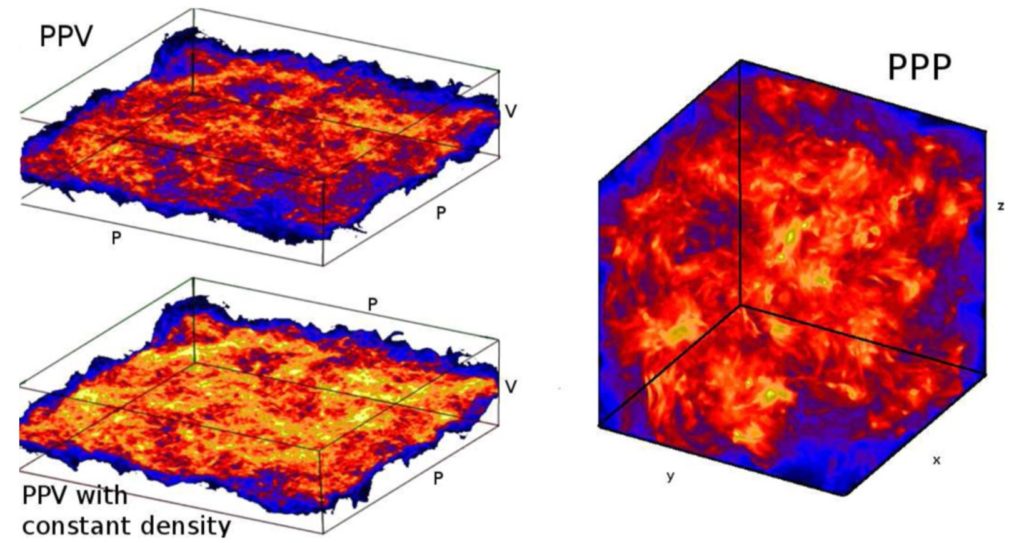
Burkhart et al. (2013) – Hierarchical Structure of Magnetohydrodynamic Turbulence in Position-position-velocity Space

Magnetohydrodynamic turbulence is able to create hierarchical structures in the interstellar medium (ISM) that are correlated on a wide range of scales via the energy cascade. We use hierarchical tree diagrams known as dendrograms to characterize structures in synthetic position-position-velocity (PPV) emission cubes of isothermal magnetohydrodynamic turbulence. We show that the structures and degree of hierarchy observed in PPV space are related to the presence of self-gravity and the global sonic and Alfvénic Mach numbers. Simulations with higher Alfvénic Mach number, self-gravity and supersonic flows display enhanced hierarchical structure. We observe a strong dependency on the sonic and Alfvénic Mach numbers and self-gravity when we apply the statistical moments (i.e., mean, variance, skewness, kurtosis) to the leaf and node distribution of the dendrogram. Simulations with self-gravity, larger magnetic field and higher sonic Mach number have dendrogram distributions with higher statistical moments. Application of the dendrogram to three-dimensional density cubes, also known as position-position-position (PPP) cubes, reveals that the dominant emission contours in PPP and PPV are related for supersonic gas but not for subsonic. We also explore the effects of smoothing, thermal broadening, and velocity resolution on the dendrograms in order to make our study more applicable to observational data. These results all point to hierarchical tree diagrams as being a promising additional tool for studying ISM turbulence and star forming regions for obtaining information on the degree of self-gravity, the Mach numbers and the complicated relationship between PPV and PPP data.

Burkhart, Blakesley; Lazarian, A.; Goodman, Alyssa; Rosolowsky, Erik
2013, The Astrophysical Journal, 770, 141
http://adsabs.harvard.edu/abs/2013ApJ…770..141B

Figure 10. Example of synthetic PPV data cubes with vertical axis being the velocity axis (left), and PPP data cube (right) for subsonic super-Alfve ́nic turbulence. Integrating along the velocity axis of PPV restores the column density map which can also be obtained from the 3D density cube. The bottom left PPV has PPP density equal to unity, and hence a constant column density. Structure in this PPV cube is due to pure velocity fluctuations. This figure highlights the need to be cautious when interpreting the structures seen in PPV. The quantitative relation between the fluctuations in PPV and underlying density and velocity fluctuations is provided in Lazarian & Pogosyan (2000).