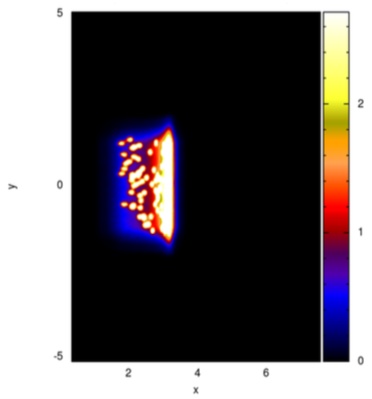
We revisit an alternate explanation for the turbulent nature of molecular clouds – namely, that velocity dispersions matching classical predictions of driven turbulence can be generated by the passage of clumpy material through a shock. While previous work suggested this mechanism can reproduce the observed Larson relation between velocity dispersion and size scale ($\sigma \propto L^{\Gamma}$ with $\Gamma \approx 0.5$), the effects of self-gravity and magnetic fields were not considered. We run a series of smoothed particle magnetohydrodynamics experiments, passing clumpy gas through a shock in the presence of a combination of self-gravity and magnetic fields. We find powerlaw relations between $\sigma$ and $L$ throughout, with indices ranging from $\Gamma=0.3-1.2$. These results are relatively insensitive to the strength and geometry of magnetic fields, provided that the shock is relatively strong. $\Gamma$ is strongly sensitive to the angle between the gas’ bulk velocity and the shock front, and the shock strength (compared to the gravitational boundness of the pre-shock gas). If the origin of the $\sigma-L$ relation is in clumpy shocks, deviations from the standard Larson relation constrain the strength and behaviour of shocks in spiral galaxies.
Forgan, Duncan H.; Bonnell, Ian A.
2018, ArXiv e-prints, 1809, arXiv:1809.06601
http://adsabs.harvard.edu/abs/2018arXiv180906601F
Context
It is well known that giant molecular clouds (GMCs) exhibit highly disordered, chaotic supersonic motions that govern the process of star formation (see e.g. McKee & Ostriker 2007, for a review). Generally speaking, these motions show evidence of energy injected into a range of size scales, a necessary characteristic of turbulence (Elmegreen & Scalo 2004).
The evidence for supersonic turbulence is boosted by the observed power-law relationship between the velocity dispersion in the gas σ at a given size scale L:
σ∝L^Γ, where Γ ≈ 0.5 (Larson 1981). Indeed, most forms of clas- sical turbulence predict a σ − L relation of some form, be it Kolmogorov turbulence (Γ = 0.33, Passot et al. 1988), Burger’s shock-driven turbulence (Γ = 0.5, Scalo et al. 1998), or She-Leveque turbulence (Γ = 0.42, She & Leveque 1994; Boldyrev et al. 2002). Dobbs & Bonnell (2007) conducted a series of numerical experiments to demonstrate that a σ − L relation can be generated in the passing of clumpy material through a shock (generated by a spiral arm for example). This “clumpy shock” origin of ISM turbulence can be seen as a combination of both gravitational instability and convergent flows, where GI forms the spiral arm that induces the shock, and the velocity differential in the gas that permits converging flows (Bonnell et al. 2013, see also Falceta- Goncalves et al. 2014).
Goal of the paper
In their work Dobbs & Bonnell (2007) simulated the flow using smoothed particle hydrodynamics (SPH) without the effects of self-gravity. They also omit magnetic fields from their analysis. Clearly these forces will shape the resultant velocity field of molecular clouds, and may significantly alter the value of Γ produced by clumpy shocked material. The authors propose to revisit these calculations using smoothed particle magneto-hydrodynamics (SPMHD), and explore the effects of both self-gravity and magnetic field on the resulting σ − L relation. There are three factors whose dependence are tested – the velocity of the gas, the shock, and the magnetic field itself.
Numerical setup
SPMHD code Phantom (Price et al. 2017)
SPH is a Lagrangian method for solving the equations of fluid dynamics assuming ideal MHD. Shocks are resolved using viscosity, conductivity and resistivity and the gravity forces are computed using a binary tree. The gas equation of state is adiabatic, with ratio of specific heats γ = 5/3. Radiative cooling prescription on the gas is not imposed here and sink creation is prohibited.
Initial conditions
Half of the box by mass is composed of uniform density gas, with the other half composed of spherical clumps, distributed randomly through the box. Each sphere has a fixed radius = 0.1, and a density 30 times the mean box density. The clumps are initially Jeans stable, with a free fall time around ten times the shock crossing time across the clump. This ensures that generation of velocity dispersion will not proceed due to the self-gravitating collapse of the clumps, but how the clumpy gas enters and leaves the shock (see section 3.3 of Dobbs & Bonnell 2007). The gas has initially zero motion in the y and z direction. The x-velocity is uniform across the gas, with velocity along x-axis = 50cs. As the box moves in the positive x-direction, it encounters a sinusoidal external potential, designed to mimic the passage of the gas through a spiral shock. The external potential is given by φ = A cos k (x + B) with A = 100 (A = 10 for a weaker shock).
Results
Control run
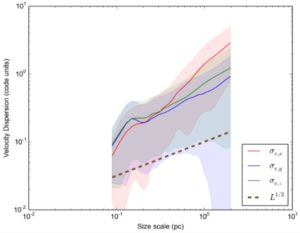
The control run of this paper is set with – Pure hydro, no self-gravity, A = 100. The clumpy structure is erased by the compressive action of the shock. The subsequent motions generated result in velocity dispersions along all three co-ordinate axes (Figure 2). As can be seen, the x-velocity (red line in Figure 2) generates the strongest dispersion, especially at large scales (note that the largest initial scale of the box is 4 pc). At scales below approximately 0.3 pc, all three velocity com- ponents show similar dispersions, and a similar scaling with L. When the material arrives at the shock head-on, the velocity dispersion along that axis tends to be boosted compared to the other axes.
Evolution of the σ − L relation
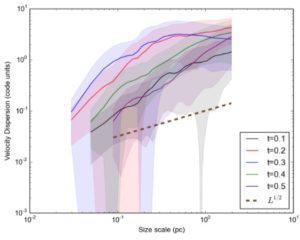
Figure 3 shows that even at a relatively early stage, a powerlaw relation is being set up in the gas that is interacting with the shock. The velocity dispersion at scales larger than rcl = 0.1 pc quickly grow, so that the dispersion relation flattens during the instant of maximum compression.
Density dependence and dependence on shock entry angle
The authors highlight that shock material is observationally observed through molecular lines. Their question is the following : How does this relationship change if we only consider the most dense material ? Simulation C and C45 runs, only counting contributions from the particles above the 30th percentile of density shows that no appreciable difference to the resulting relations, or the fits to Γ in vx , vy or vz . Importantly, there was no appreciable change in the scatter derived in this relation.
When shock front is rotated by 45 degree around the z-axis. The velocity dispersion unsurprisingly increases in the y direction. The velocity dispersion in z remains unchanged.
Strong shock (CW) vs. weak shock (C)
As might be expected, reducing the shock strength by a factor of ten also reduces the resulting velocity dispersions generated, as can be seen by comparing the C and CW runs. The amplitude of σ decreases at all scales by around a factor of 2, and the resulting Γ is also generally lower. This becomes quite extreme if self-gravity is activated. The weakness of the shock delivers correspondingly weak compression of the clumpy gas. As a result, the post shock gas retains more of its original clumpy structure, and the ensuing velocity dispersion is being generated by the gravitational collapse of this compressed material. Reducing the shock amplitude A with self-gravity active (SGW) tends to flatten the relation, resulting in very low Γ values. A similar result is achieved if A is fixed at its control value, but the total mass of the shocked material is changed. This indicates that Γ is controlled by the relationship between the boundness of the gas pre-shock and the depth of the spiral potential. This is consistent with the emerging picture from global simulations of molecular cloud formation in spiral structures (e.g. Jin et al. 2017), where molecular cloud turbulence parameters assume a spectrum of values depending on the details of their shock ingress/egress.
MHD runs without self-gravity
The resulting σ − L relations are similar to the control run. This suggests that magnetic pressure is playing a limited role in resisting gas compression, even when the magnetic pressure and thermal pressure are initially equal (βp = 1). Furthermore, the authors suggest that the depth of the potential is sufficiently large to make ideal MHD effects irrelevant in the generation of a velocity dispersion relation through spiral shocks. To check this, they repeat the simulation, but reduce the shock strength A from 100 to 10. they find that the resulting best fit Γ profiles are similar to the same simulation without magnetic fields (CW), but that velocity dispersion in x becomes flat beyond r > 0.3 pc, at a value of around 0.2 code units, as compression in the shock is now being effectively resisted by magnetic pressure, as expected. This therefore indicates that in this model, MHD effects are only important when the spiral shock becomes relatively weak.
MHD runs with self-gravity
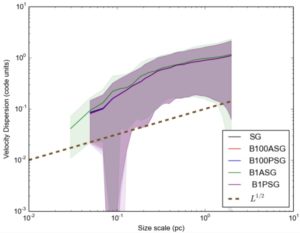
Figure 8 shows the σ − L relations for all five runs, and there is little difference between them.
Shock angle vs magnetic field angle
As seen before, the pure hydrodynamic runs that modifying the shock entry angle mixes the velocity dispersion evenly between co-ordinate systems. How does altering the direction of the field affect this mixture ? The simulation B100-45 show that the B-field orientation makes little appreciable effect to the fits for Γ, which are comparable to those for the B100A runs.