In this letter we present numerical and experimental results on the scaling properties of velocity turbulent fields in the range of scales where viscous effects are acting. A generalized version of extended self-similarity capable of describing scaling laws of the velocity structure functions down to the smallest resolvable scales is introduced. Ourfindings suggest the absence of any sharp viscous cut-off in the intermittent transfer of energy.
Benzi, R.; Biferale, L.; Ciliberto, S.; Struglia, M. V.; Tripiccione, R.
1995, eprint arXiv:chao-dyn/9509008
http://adsabs.harvard.edu/abs/1995chao.dyn..9008B
Context
The word anomalous scaling (AS) usually refers to scaling laws in a physical system which cannot be deduced from naive dimensional arguments. It is always a challenging problem in physics to understand the origin of anomalous scaling and to formulate a predictive theoretical framework to compute the anomalous-scaling exponents.
Among the many physical systems showing anomalous scaling, fully developed three-dimensionalturbulence (FDT) has been widely investigated in the last fewyears (see FRISCH U., Turbulence: The Legacy of A N. Kolmogmv (Cambridge University Press) 1995.) for a recent overview of the experimental and theoretical state of the art). According to Kolmogorov 1941 theory[2], the small-scale statistical properties of FDT obey the relation
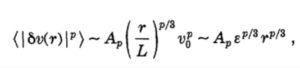where S v(r)=v(x+r)-v(x) is the difference of velocity at scale r, v0 is the r.m.s. velocity at the integral scale L, E is the mean energy dissipation and the Ap’s are dimensionless constants. Equation (1) is not satisfied both in real experiments and numerical simulation. Indeed, one has to replace it by anomalous (also known as intermittent) scaling
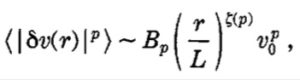
where the new exponent is now a non-linear function of its argument.
Goal of the letter
To highlight this anomalous scaling, it has been proposed in [Benzi R. 1993, Phys. Rev E, 48 (1993) R29, Benzi R. 1993, Europhyys. Lett., 24 (1993) 275.] to look at the self-sealing properties of the velocity structure functions. This almost universal property of turbulent flows was then called Extended Self-similarity (ESS). ESS must be interpreted asthe signature of some non-trivial universal physics happening at the transition between the inertial and viscous scale. It tells us that, by using the appropriate functional form, scaling is present also at scales where in principle viscous effects should already be important. The aim of this letter is to present a generalized version of ESS (GESS)which turns out to be much more universal and allows us to draw a concrete theoretical framework of the energy cascade down to the smallest resolvable scale, ie. in a region where no anomalous scaling was supposed to be detected.
Results
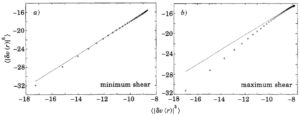
previous case ESS is not observed.
The authors show that it is clear from fig. la) that ESS is observed for the case of minimum shear and it is not observed for the case of maximum shear (fig. lb)). They propose to a new dimensionless structure functions
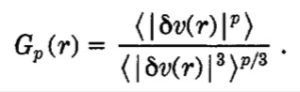
Their main point consists in studying the self-sealing properties of this dimensionless structure functions, namely for any p and q, they consider the scaling relation
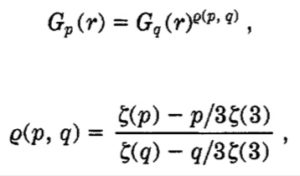
rho(p,q) is given by the ratio between deviations from the K41 scaling. It turns out that the self-sealing associated define previously (hereafter referred to as G-ESS) works perfectly well at all resolvable scales even in case maximum shear, as can be seen in fig. 2.
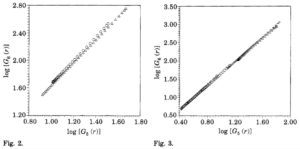
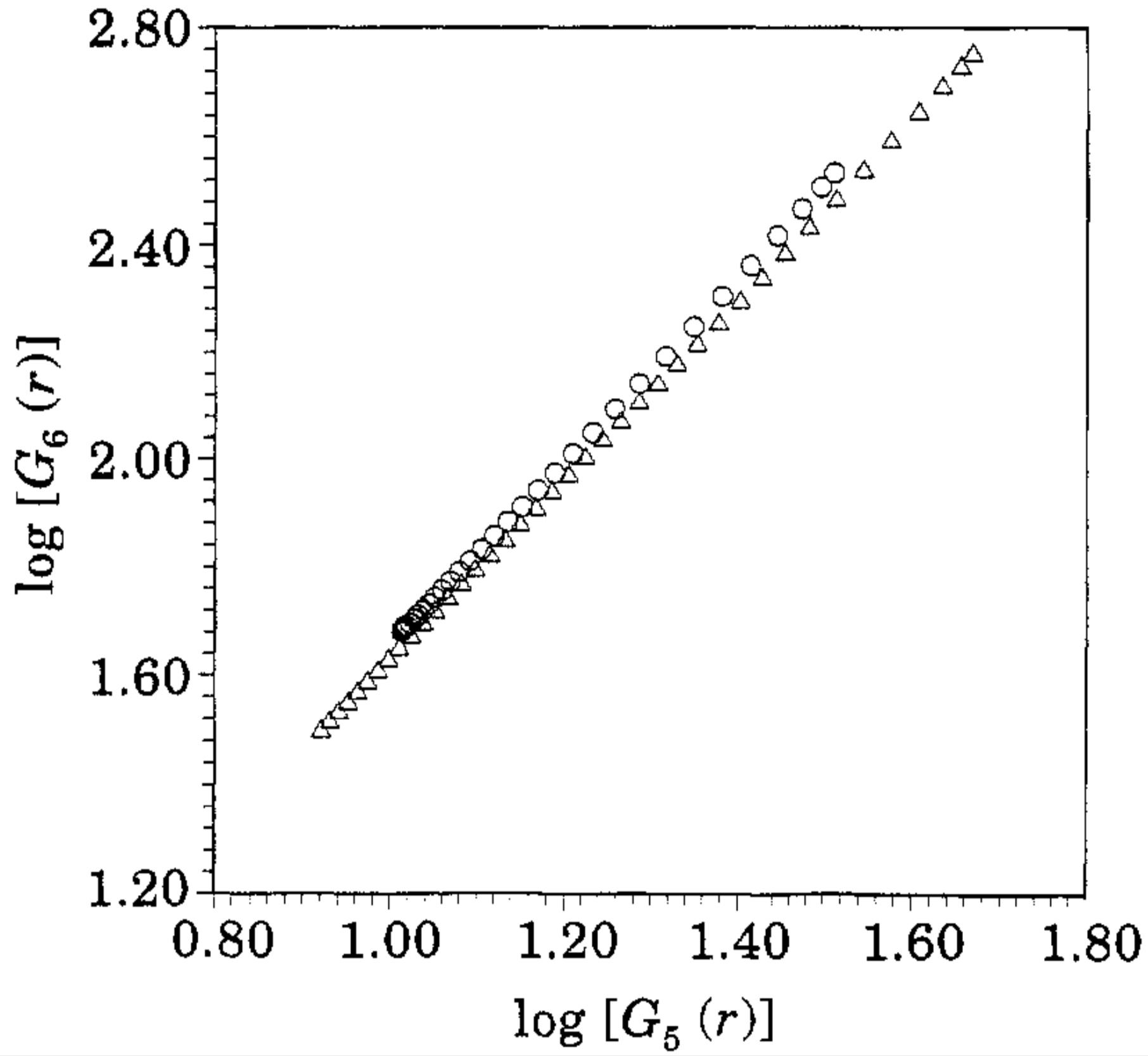
Fig. 3. – Log-log plot of G6( T ) vs.GS( T ) for different laboratory and numerical experiments. Data taken in a wake behind a cylinder, where standard ESS was not observed [3] (crosses). Data taken from the region with log-profle of a boundary layer (courtesy of G. Ruiz Chavarria) where standard ESS was not observed (circles). Data taken from a direct numerical simulation of thermal convection[S] where standard ESSwas observed (squares). Data from a direct numerical simulation of a channel flow where standard ESS was not observed[91 (triangles).
The physical outcome of their findings is that whatever is the mechanism responsible for anomalous scaling in FDT, this mechanism is acting also at extremely small scales and, within experimental errors, no evidence of a cut-off (due to dissipation) is observed. Finally, the authors remark a possible theoretical interpretation of G-ESS based on a recent model proposed in [SHE Z. S. and LEVEQUE E., Phys. Rev. Lett., 72 (1994) 336.]. In their study, the anomalous exponents are well fitted by a function related to h0 and do, free parameters describing the geometric nature of the coherent structures in turbulent flows and Beta the non-linear intermittent energy transfer. It follows form the anomalous exponent,
the relation
Indeed, one can think that the geometric characteristic of the coherent structures (defined in terms of ho and do) can be scale dependent while the non-linear intermittent energy transfer (parametrized by Beta) is scale independent.